Moment of Inertia (MOI) is a fascinating part of mass properties. The change in MOI is what makes the ice skater spin faster when he/she draws his/her arms towards the body. It is a physical experience any clerks sitting on a rotating office chair can test out for themselves.
A more scientific definition of MOI can be put forth as: A measure of an object’s resistance to changes in its rotation rate. It is the rotational analog of mass.
A change in the rotation rate is also a change to the object’s acceleration. And this is where it gets interesting for a vessel as the MOI says something about the resistance to the vessel’s acceleration around its axes, or to put it very plainly: How “stiff” will the vessel act when it rolls, yaws and pitches.
Of course, there are other factors contributing to this “stiffness”, like hull shape, stability, anti-rolling tanks and so on – but the MOI is the object’s ” stiffness”-property as defined by the mass distribution of the object and not affected by the sea or other external forces.
Thus, the MOI of a vessel is core to being able to calculate seakeeping and sea motion for any vessel. But the task is not very straightforward, as an accurate calculation of the MOI is done by integrating the mass over its distribution, a task that even modern CAD tools will struggle with, even if the vessel is completely modelled in CAD at the point where the MOI values are needed (which rarely, if ever, happens).
This is where the parallel axis theorem (also known as Huygens-Steiner theorem) comes to the rescue. This theorem defines the transferred inertia of an object, meaning the inertia around a different (global) axis than the object’s own (local) axis. It is calculated by squaring the distance between the global and local axis and multiplying it with the object’s mass. The trick to calculate MOI for a vessel then becomes to divide it into several objects and summarize the transferred inertia for all objects as an approximation for the total vessel.
The accuracy of this method depends upon how many objects you divide the vessel into and how large these objects are. A further approximation to the accurate answer can be calculated by adding each of the object’s local inertia to the transferred inertia using the known formula for a solid cuboid as an approximation.
| Solid cuboid of height h, width w, and depth d, and mass m | 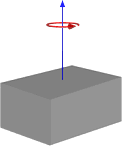 | 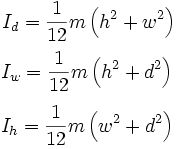 |
Solid cuboid inertia (source: en.wikipedia.org)
ShipWeight uses the parallel axis theorem, optionally combined with a user-input value of the object’s actual MOI or a solid cuboid approximation, to calculate the MOI of a vessel. How this is done can be seen in our tutorial video #8: Basic Additional Features, available on ShipWeight’s YouTube channel and on our website https://shipweight.com/videos

